Su Dalgaları konu anlatımı ile fizik öğrenin! Dalgaların dünyasına dalın ve konuyu detaylıca anlayın. İpuçları için tıklayın.
Su Dalgası
Su yüzeyine atılan bir taşın ya da yatay olarak suya daldırılan bir cetvelin ileri geri hareketi sonucunda su yüzeyinde oluşan dalgalara su dalgaları denir.
- Su dalgalarının yayılabilmesi için maddesel ortam gereklidir. Bu nedenle su dalgaları mekanik dalgalardır
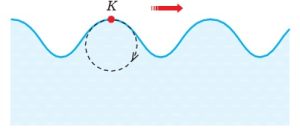
- Su molekülleri hem enine hem de boyuna titreşimin birleşimi sonucu şekildeki gibi çembersel titreşim hareketi yaptığı için, su dalgaları enine ve boyuna dalgaların birleşimi olan özel bir dalgadır. Şekildeki su dalgaları ok yönünde ilerlerken, dalga yüzeyindeki bir K noktası hem yukarı aşağı hem de sağa sola titreşim yapmaktadır.
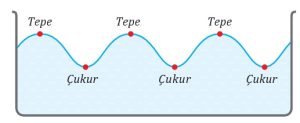
- Su dalgaları üzerindeki en yüksek noktaya dalga tepesi, en alt noktaya dalga çukuru denir.
- Su dalgalarını incelemek için kullanılan, camdan yapılmış deney kabına dalga leğeni denir.
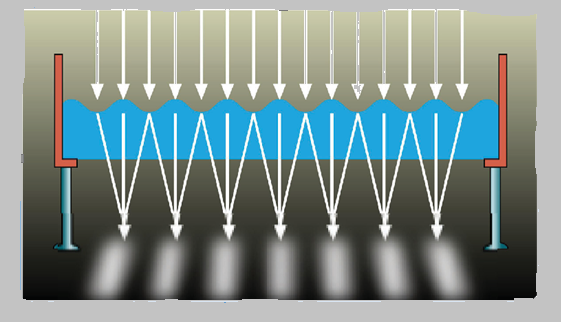
- Su dalgaları incelenirken üstten ışık gönderilir. Dalga tepeleri ince kenarlı mercek gibi davranarak ışığı toplar, dalga çukurları ise kalın kenarlı mercek gibi davranarak ışığı dağıtır. Bu nedenle şekildeki gibi dalga tepeleri zeminde aydınlık, dalga çukurları ise zeminde karanlık şeritler meydana getirir.
- Durgun su yüzeyinde oluşan dalgalar, kullanılan kaynağa göre doğrusal veya dairesel yayılır.
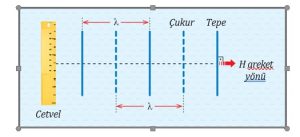
- Bir cetvelin yatay olarak suya batırılıp çıkarılması ile elde edilen dalgalara doğrusal su dalgası denir. Şekildeki gibi kalın çizgi ile gösterilen kısımlar dalga tepelerini, kesikli çizgi ile gösterilen kısımlar dalga çukurlarını belirtir. Bu dalgalar tepe çizgilerine dik olarak yayılır. İki dalga tepesi ya da iki dalga çukuru arasındaki uzaklık dalga boyu (Α) kadardır.
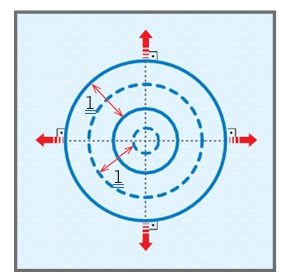
- Bir kalemin sivri ucunun suya batırılıp çıkarılması ile elde edilen dalgalara dairesel su dalgaları denir. Şekildeki gibi kalın çizgi ile gösterilen kısım dalga tepelerini, kesikli çizgi ile gösterilen kısım dalga çukurlarını belirtir. Oluşan dairesel dalgaların merkezi, kalemin su yüzeyine ilk temas ettiği noktadır. Dairesel su dalgaları aynı merkezli, genişleyen daireler halinde yayılır.
Doğrusal ve Dairesel Su Dalgalarında Yansıma
- Dalga leğeninde yapılan deneylerde su dalgalarının düzlem ve parabolik engellerden yansımasının, yansıma kanunlarına uyduğu gözlenmiştir.
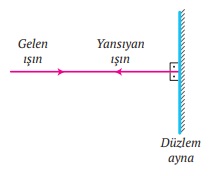
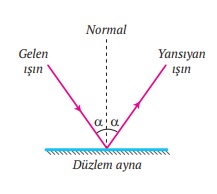
- Işığın yansıma kanunlarına göre, ışığın bir yüzeye çarpıp geri dönmesi olayına yansıma denir.
- Yansıma olayında gelen ışık yüzey normali ile kaç derece açı yapıyorsa, yansıyan ışık da yüzey normali ile aynı açıyı yapar.
Doğrusal Su Dalgalarının Doğrusal Engelden Yansıması
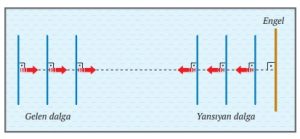
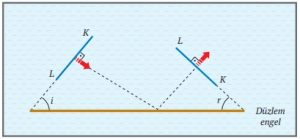
- Doğrusal su dalgasının geliş doğrultusu düzlem engelin yüzey normali ile çakışıyorsa, doğrusal su dalgaları şekildeki gibi geliş doğrultusunda geri yansır.
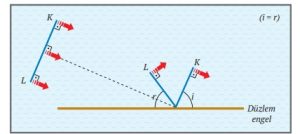
- Doğrusal su dalgasının, gelen kısmının düzlem engelle yaptığı açı ile yansıyan kısmının düzlem engelle yaptığı açı birbirine eşittir. Gelen dalganın engelle yaptığı açıya gelme açısı (i), yansıyan dalganın engelle yaptığı açıya yansıma açısı (r) denir.
- Doğrusal su dalgasının engelle yaptığı açı i ise, doğrusal su dalgası şekildeki gibi r açısı yaparak yansır. (i = r)
Doğrusal Su Dalgalarının Parabolik Engelin Çukur Yüzeyinden Yansıması
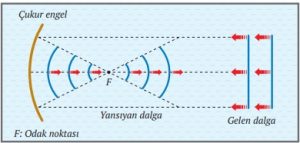
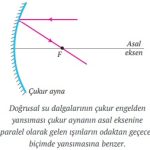
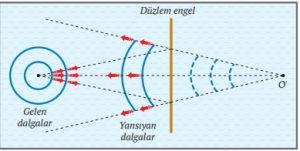
Parabolik engelin çukur yüzeyine gönderilen doğrusal su dalgaları, engelden yansıdığında şekildeki gibi önce parabolik engelin odak noktasında toplanır sonra dairesel dalgalar biçiminde yayılır.
Doğrusal Su Dalgalarının Parabolik Engelin Tümsek Yüzeyinden Yansıması
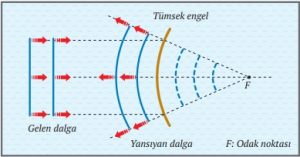
Parabolik engelin tümsek yüzeyine gönderilen doğrusal su dalgaları engelden yansıdığında şekildeki gibi engelin arkasındaki bir noktadan üretilen dairesel dalgalar biçiminde yayılır.
Dairesel Su Dalgalarının Düzlem Engelden Yansıması
Düzlem engele gelen dairesel su dalgaları engelden yansıdığında şekildeki gibi engelin arkasındaki bir noktadan geliyormuş gibi yayılır.
Dairesel Su Dalgalarının Parabolik Engelin Çukur Yüzeyinden Yansıması
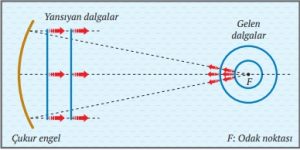
Çukur engelin odağındaki bir kaynaktan gönderilen dairesel su dalgaları yansıdığında şekildeki gibi doğrusal su dalgaları olarak yayılır.
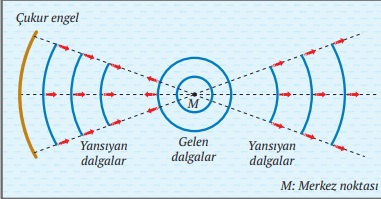
Çukur engelin merkezindeki bir kaynaktan gönderilen dairesel su dalgaları yansıdığında şekildeki gibi önce parabolik engelin merkez noktasında toplanır sonra dairesel dalgalar biçiminde yayılır.