Mutlak Değer Konu Anlatımı ile matematikteki bu önemli kavramı daha iyi anlayın. Temel matematik bilgisi.
A. TANIM
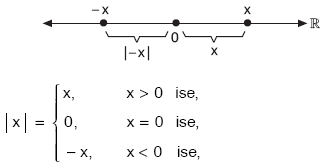
Sayı doğrusu üzerinde x reel (gerçel) sayısının orijine olan uzaklığına x in mutlak değeri denir.
|x| biçiminde gösterilir.
| Bütün x gerçel (reel) sayıları için, |x| ³ 0 dır. |
B. MUTLAK DEĞERİN ÖZELİKLERİ
- |x| = |–x| ve |a – b| = |b – a| dır.
- |x × y| = |x| × |y|
- |xn| = |x|n
- y ¹ 0 olmak üzere,
- |x| – |y| £ |x + y| £ |x| + |y|
- a ³ 0 ve x Î
olmak üzere,
|x| = a ise, x = a veya x = –a dır.
- |x| = |y| ise, x = y veya x = –y dir.
- x değişken a ve b sabit birer reel (gerçel) sayı olmak üzere,
|x – a| + |x – b|
ifadesinin en küçük değeri a £ x £ b koşuluna uygun bir x değeri için bulunan sonuçtur.
- x değişken a ve b sabit birer reel (gerçel) sayı ve
K = |x – a| – |x – b|
olmak üzere,
x = a için K nin en küçük değeri, x = b için K nin en büyük değeri bulunur.
- a, pozitif sabit bir reel sayı olmak üzere,
a) |x| < a ise, –a < x < a dır.
b) |x| £ a ise, –a £ x £ a dır.
- a, pozitif sabit bir reel sayı olmak üzere,
a) |x| > a ise, x < –a veya x > a dır.
b) |x| ³ a ise, x £ –a veya x ³ a dır.
- a < b ve c Î
olmak üzere,
|x + a| + |x + b| = c
eşitliğinin çözüm kümesini bulmak için 2 yöntem vardır.
1. Yöntem
Mutlak değerlerin içlerinin kökleri bulunur.
x + a = 0 ise, x = –a dır.
x + b = 0 ise, x = –b dir.
Buna göre, üç durum vardır. (–b < –a olsun.)
–b £ x, –b < x £ –a ve x > –a dır. Bu üç durumda inceleme yapılır.
1. Durum
–b £ x ise, –x – a – x – b = c olur. Bu denklemin kökü –b £ x koşulunu sağlıyorsa, verilen denklemin de köküdür.
2. Durum
–b < x £ –a ise, –x – a + x + b = c olur.
Bu denklemin kökü –b < x £ –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3. Durum
x > –a ise, x + a + x + b = c olur. Bu denkleminin kökü x > –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3 durumdan elde edilen köklerin oluşturacağı küme, verilen denklemin çözüm kümesidir.
2. Yöntem
a < b ve c Î
olmak üzere,
|x + a| + |x + b| = c … (¶)
eşitliğinin çözüm kümesinde aşağıdaki üç durum geçerlidir.
(x + a = 0 ise, x = –a) ve (x + b = 0 ise, x = –b)
- Sayı doğrusunda –b ile –a arasındaki uzaklık c ye eşit ise,
(¶) daki denklemin çözüm kümesi,
Ç = [–b, –a] dır.
- Sayı doğrusunda –b ile –a arasındaki uzaklık c den büyük ise,
(¶) daki denklemin çözüm kümesi,
Ç = Æ dir.
- Sayı doğrusunda –b ile –a arasındaki uzaklık c den küçük ise,
(¶) daki denklemi sağlayan iki sayı vardır. Bu sayıları bulmak için, c den, sayı doğrusunda –b ile –a arasındaki uzaklık çıkarılır, farkın yarısı bulunur. Son bulunan değer D olsun. Buna göre, (¶) daki denklemi sağlayan sayılardan biri –b – D diğeri –a + D dir. Bu durumda (¶) daki denklemin çözüm kümesi,
Ç {–b – D, –a + D}






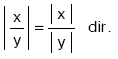
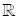 olmak üzere,
olmak üzere, olmak üzere,
olmak üzere,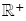 olmak üzere,
olmak üzere,


