YÜKSEK SAYILARI ÇARPMAK ARTIK KABUS DEĞİL!
Matematik korkulu rüyanız olmaktan çıksın. Çünkü onunla ilgilenmeye başladıkça bazı şeylerin aslında o kadar da zor olmadığını görüyorsunuz. Bu mükemmel Japon tekniği, ise büyük sayılarla yapılan çarpma işlemleriniz için eğlenceli bir yol sunuyor.
Büyük sayılar, çocukluk yaşlarında oluşan matematik fobisinin fitili ateşlerler. Onlarla yapılan işlemler her zaman karışık gelebilir. Eğer matematiği öğrenmeye başladığınız ilk kişi sizin bu işlerden ne kadar zevk aldığınızı önemsemiyorsa, bu fobiyi ömür boyu taşıyabilirsiniz.
Fakat matematik hayatın kendisidir ve rakamlar, hayatınızın bir nano saniyesinde bile sizi yalnız bırakmazlar. Bu nedenle hangi mesleğe hevesli olursanız olun, hangi işle ilgilenirseniz ilgilenin matematik, size bambaşka bakış açıları kazandırabilecek, ufkunuzu genişletecek bir yapıya sahiptir.
Japonlar matematik konusunda toplumsal olarak en başarılı insanlardandır. Bunun altında büyük bir disiplin yatsa da keşfettikleri sayısız yöntem, başarılarını beraberinde getirmiştir.
Birbiriyle kesişen çizgilerin, çarpma işlemlerinde çok işe yarayacağını Japonlardan başka kim tahmin edebilirdi ki?
Yukarıda gördüğünüz ilk örnek olan 3 x 2 = ? işleminde aslında temel mantığı kavrıyoruz. Birbirine paralel 3 çizgiyi, onları kesecek şekilde çizdiğimiz 2 çizgiyle işi daha kolay işlemlere devrediyoruz. Kesişme noktalarını saydığımızda ise soncunun 6 olduğunu görüyoruz. Peki çok basamaklı sayılarda bu yöntem nasıl kullanılıyor?
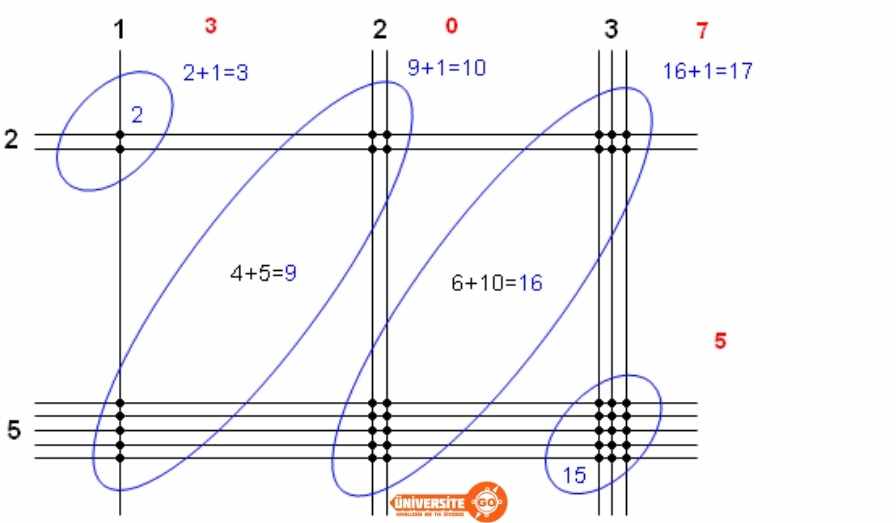
Resimdeki ikinci örnekte gördüğümüz 123 x 25 = ? işlemi için ilk ifadedeki rakamları dikey, ikinci ifadedeki rakamları yatay olarak çiziyoruz. Fakat bu kez kesişme noktalarırımız birden fazla bölgede toplanıyor. Yapmamız geren bu noktaları, sol üst köşeden başlayarak saymak. Bu aşamada dikkat etmeniz gereken bir nokta var: Köşegenler. Ortaya çıkan keşişmeleri sol alt köşeden sağ üst köşeye doğru gruplandırılıyoruz. Sonra sırasıyla bu gruplardaki kesişme sayılarını yazıyoruz.
Eğer gruplardaki kesişme sayıları gene iki rakamlı bir sayı olursa, o rakamları da birbirleriyle topluyoruz. Örnekteki 16 kesişme olan grubu 1 + 6 = 7 şeklinde sonuca dahil ediyoruz.
Bir dip not bu gruplardan herhangi birinin sonucu 10 çıkarsa, istisnai olarak o grubu 0 şeklinde kabul ediyoruz. Aksi takdirde sonucumuz hatalı olur.
Yapacağımız son adım ise kesişme gruplarındaki rakamları yan yana yazmak oluyor:
123 x 25 = ? işleminin sonucunu, sol üst köşeden sağ alt köşeye doğru okuyoruz. Yani işlemin sonucu 3075 olarak karşımıza çıkıyor.
123 x 25 = 3075





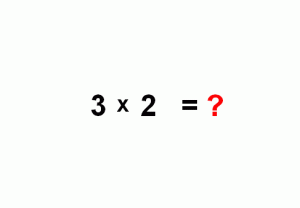




hocam fotoğraflar da olsaydı anlayacaktık da . uygulamada görünmüyordu bilgisayardan bakayım dedim burada da aynı
Ben okurken tam anlayamadim gorsellerle daha aciklayici olabilirdi